How to Draw a Cartesian Plane in Latex
When I started working on my thesis dissertation using LaTeX, I discovered the TikZ package for drawing vector-based figures. I needed a way to hands depict iii-dimensional figures, and so I put together a few handy tools in the tikz-3dplot package. This package builds on TigZ, providing an piece of cake fashion to rotate the perspective when cartoon three-dimensional shapes using basic shapes in a tikzpicture environment.
Let'southward explore some examples of what tikz-3dplot tin can exercise.
– A contribution to the LaTeX and Graphics contest – This article is available for reading and for download in pdf format –
The Basics
Let'due south draw a cube, with side length of 2. To aid illustrate the comparison, we'll describe a grid in the ten–y plane, and also show the 10, y, and z axes.
\begin{tikzpicture} [cube/.style={very thick,blackness}, filigree/.way={very thin,greyness}, axis/.style={->,blue,thick}] %draw a grid in the x-y plane \foreach \x in {-0.five,0,...,ii.five} \foreach \y in {-0.5,0,...,ii.5} { \draw[grid] (\x,-0.five) -- (\10,two.5); \draw[grid] (-0.five,\y) -- (2.5,\y); } %draw the axes \draw[centrality] (0,0,0) -- (3,0,0) node[anchor=west]{$x$}; \draw[axis] (0,0,0) -- (0,3,0) node[ballast=west]{$y$}; \draw[axis] (0,0,0) -- (0,0,3) node[anchor=west]{$z$}; %draw the height and bottom of the cube \draw[cube] (0,0,0) -- (0,2,0) -- (ii,2,0) -- (2,0,0) -- wheel; \draw[cube] (0,0,2) -- (0,ii,2) -- (2,ii,2) -- (2,0,2) -- cycle; %draw the edges of the cube \draw[cube] (0,0,0) -- (0,0,2); \depict[cube] (0,2,0) -- (0,2,two); \draw[cube] (2,0,0) -- (ii,0,2); \draw[cube] (2,two,0) -- (two,2,ii); \cease{tikzpicture} \tdplotsetmaincoords{60}{125} \begin{tikzpicture} [tdplot_main_coords, cube/.style={very thick,black}, grid/.style={very thin,gray}, centrality/.fashion={->,blue,thick}] %depict a grid in the x-y plane \foreach \x in {-0.5,0,...,2.v} \foreach \y in {-0.5,0,...,two.5} { \describe[grid] (\ten,-0.v) -- (\x,2.5); \draw[grid] (-0.5,\y) -- (ii.5,\y); } %depict the axes \draw[axis] (0,0,0) -- (3,0,0) node[ballast=west]{$x$}; \draw[axis] (0,0,0) -- (0,3,0) node[anchor=west]{$y$}; \depict[axis] (0,0,0) -- (0,0,3) node[anchor=west]{$z$}; %depict the top and lesser of the cube \depict[cube] (0,0,0) -- (0,2,0) -- (2,ii,0) -- (two,0,0) -- cycle; \depict[cube] (0,0,2) -- (0,2,2) -- (2,2,2) -- (ii,0,2) -- cycle; %draw the edges of the cube \draw[cube] (0,0,0) -- (0,0,2); \depict[cube] (0,ii,0) -- (0,2,2); \draw[cube] (2,0,0) -- (2,0,2); \depict[cube] (2,2,0) -- (2,ii,2); \end{tikzpicture} 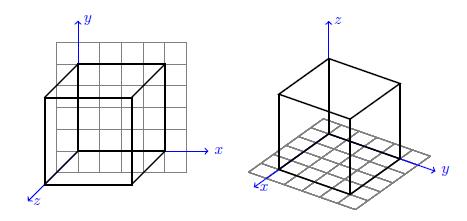
In the default configuration, shown on the left, the xy plane lies in the same airplane equally the page. The z-centrality extends downwards and to the left, giving the illusion of depth. This is a useful representation of a 3-dimensional infinite as is, but gives little in the range of customization.
The tikz-3dplot package can redefine the perspective for viewing this three-dimensional space. In the tikz-3dplot configuration, the z-axis points in the vertical direction, and the viewed perspective of the xy plane tin be specified using the user-specified values θ and φ (in degrees). These angles ascertain the direction from which the three-dimensional infinite is viewed, using the standard definition of the polar and azimuthal angles from polar coordinates.
To specify the display orientation, utilise the command \tdplotsetmaincoords{θ}{φ} before the tikzpicture environs, and include the tdplot_main_coords style within any drawing control. Alternatively, as seen in this example, you lot can include the tdplot_main_coords style within the global style settings of the tikzpicture environment.
As suggested by the name, tdplot_main_coords, I refer to this coordinate frame as the "main" coordinate frame. It provides the base through which you tin perform all cartoon operations. It may seem a fleck restrictive that the z-axis of the chief coordinate frame tin can merely the vertical direction. If you wish to define a more general orientation, at that place is a second, "rotated" coordinate frame that can exist specified relative to the orientation of the primary coordinate frame. Allow'southward take a look at this cube example again, drawn in the rotated coordinate frame.
\tdplotsetmaincoords{lx}{120}% \tdplotsetrotatedcoords{0}{20}{0}% \brainstorm{tikzpicture} [tdplot_rotated_coords, cube/.style={very thick,black}, filigree/.fashion={very thin,grey}, axis/.way={->,blue,thick}, rotated centrality/.style={->,purple,thick}] %draw a grid in the x-y plane \foreach \ten in {-0.5,0,...,2.5} \foreach \y in {-0.5,0,...,2.5} { \draw[filigree] (\x,-0.v) -- (\ten,2.5); \depict[grid] (-0.5,\y) -- (ii.5,\y); } %draw the master coordinate frame axes \describe[axis,tdplot_main_coords] (0,0,0) -- (3,0,0) node[anchor=due west]{$x$}; \depict[axis,tdplot_main_coords] (0,0,0) -- (0,three,0) node[anchor=northward west]{$y$}; \draw[axis,tdplot_main_coords] (0,0,0) -- (0,0,3) node[anchor=w]{$z$}; %describe the rotated coordinate frame axes \depict[rotated centrality] (0,0,0) -- (three,0,0) node[ballast=west]{$x'$}; \draw[rotated axis] (0,0,0) -- (0,3,0) node[anchor=south west]{$y'$}; \draw[rotated axis] (0,0,0) -- (0,0,3) node[anchor=w]{$z'$}; %draw the top and bottom of the cube \draw[cube] (0,0,0) -- (0,ii,0) -- (2,2,0) -- (two,0,0) -- bicycle; \draw[cube] (0,0,ii) -- (0,2,two) -- (2,2,two) -- (2,0,2) -- bicycle; %draw the edges of the cube \draw[cube] (0,0,0) -- (0,0,two); \describe[cube] (0,ii,0) -- (0,2,2); \draw[cube] (2,0,0) -- (2,0,2); \draw[cube] (2,2,0) -- (two,2,2); \terminate{tikzpicture} 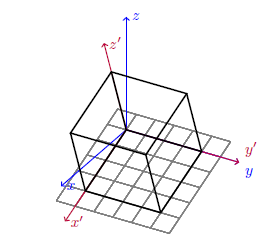
Here, I show the axes for both the main coordinate frame (xyz) and rotated coordinate frame (10'y'z'). Using the control \tdplotsetrotatedcoords{θz }{θy }{θz }, the rotated coordinate frame is defined by taking the orientation of the primary coordinate frame, and then performing the Euler bending rotations (θz, θy, θz) (in degrees) to ascertain the rotated coordinate frame. The coordinate transformation for the rotated coordinate frame is stored in the tdplot_rotated_coords manner. In this instance, I simply rotated about the y-axis of the main coordinate frame.
Examples
Defining tdplot_main_coord and tdplot_rotated_coords is just the beginning. tikz-3dplot provides a agglomeration of handy tools to go far easier to work in a three-dimensional space.
Defining Coordinates
For example, the control \tdplotsetcoord{ r }{θ}{φ} defines a coordinate using spherical coordinates r, θ, φ. More than that, this handy command also defines points that can be useful for projections on the axes and their shared planes. Consider the following example, where the coordinate (P) is divers in the three-dimensional space using spherical polar coordinates.
\tdplotsetmaincoords{threescore}{120} \begin{tikzpicture} [scale=3, tdplot_main_coords, centrality/.way={->,blue,thick}, vector/.style={-stealth,crimson,very thick}] %standard tikz coordinate definition using x, y, z coords \coordinate (O) at (0,0,0); %tikz-3dplot coordinate definition using r, theta, phi coords \tdplotsetcoord{P}{.8}{55}{lx} %depict axes \draw[axis] (0,0,0) -- (1,0,0) node[anchor=north east]{$ten$}; \draw[centrality] (0,0,0) -- (0,1,0) node[anchor=north westward]{$y$}; \draw[axis] (0,0,0) -- (0,0,i) node[anchor=due south]{$z$}; %draw a vector from O to P \draw[vector] (O) -- (P); \end{tikzpicture} \tdplotsetmaincoords{60}{120} \brainstorm{tikzpicture} [scale=three, tdplot_main_coords, axis/.style={->,blue,thick}, vector/.manner={-stealth,red,very thick}, vector guide/.fashion={dashed,cherry,thick}] %standard tikz coordinate definition using 10, y, z coords \coordinate (O) at (0,0,0); %tikz-3dplot coordinate definition using r, theta, phi coords \tdplotsetcoord{P}{.8}{55}{60} %draw axes \depict[axis] (0,0,0) -- (1,0,0) node[anchor=north east]{$x$}; \draw[axis] (0,0,0) -- (0,1,0) node[anchor=north west]{$y$}; \draw[axis] (0,0,0) -- (0,0,1) node[ballast=south]{$z$}; %draw a vector from O to P \depict[vector] (O) -- (P); %describe guide lines to components \draw[vector guide] (O) -- (Pxy); \describe[vector guide] (Pxy) -- (P); \finish{tikzpicture} 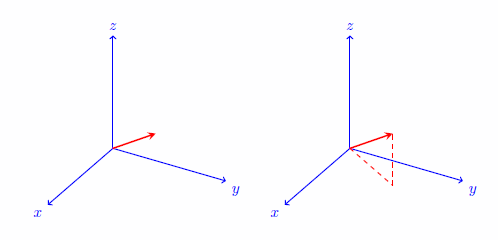
In the left diagram, information technology is hard to identify where the vector lies in the iii-dimensional space. In the right diagram, I make use of the (automatically generated) projection coordinate (Pxy), which lies in the xy plane below (P), to illustrate the orientation of the vector.
Cartoon Circles and Arcs
To describe a circle or arc, the \tdplotdrawarc command is provided. Here, you specify the eye of the circle/arc, the radius, the showtime and end angles, and characterization notes. Here are a couple examples that apply arcs and circles.
\tdplotsetmaincoords{lx}{120} \brainstorm{tikzpicture} [scale=3, tdplot_main_coords, centrality/.style={->,blue,thick}, vector/.fashion={-stealth,blood-red,very thick}, vector guide/.style={dashed,red,thick}, angle/.fashion={red,thick}] %standard tikz coordinate definition using x, y, z coords \coordinate (O) at (0,0,0); %tikz-3dplot coordinate definition using r, theta, phi coords \tdplotsetcoord{P}{.8}{55}{sixty} %describe axes \draw[axis] (0,0,0) -- (1,0,0) node[anchor=north eastward]{$10$}; \draw[axis] (0,0,0) -- (0,1,0) node[anchor=north w]{$y$}; \draw[axis] (0,0,0) -- (0,0,1) node[anchor=south]{$z$}; %describe a vector from O to P \draw[vector] (O) -- (P); %draw guide lines to components \depict[vector guide] (O) -- (Pxy); \draw[vector guide] (Pxy) -- (P); %depict an arc illustrating the angle defining the orientation \tdplotdrawarc[angle]{(O)}{.35}{0}{60}{anchor=north}{$\phi$} %define the rotated coordinate frame to lie in the "theta plane" \tdplotsetthetaplanecoords{55} \tdplotdrawarc[tdplot_rotated_coords,bending]{(O)}{.35}{0}{55} {ballast=south west}{$\theta$} \end{tikzpicture} \tdplotsetmaincoords{55}{5} \begin{tikzpicture} [scale=3, tdplot_main_coords, curve/.style={crimson,densely dotted,thick}] \coordinate (O) at (0,0,0); \foreach \bending in {-xc,-75,...,90} { %calculate the sine and cosine of the angle \tdplotsinandcos{\sintheta}{\costheta}{\angle}% %define a point along the z-axis through which to depict %a circle in the xy-plane \coordinate (P) at (0,0,\sintheta); %describe the circle in the master frame \tdplotdrawarc[curve]{(P)}{\costheta}{0}{360}{}{} %define the rotated coordinate frame based on the angle \tdplotsetthetaplanecoords{\angle} %depict the circle in the rotated frame \tdplotdrawarc[curve,tdplot_rotated_coords]{(O)}{1}{0}{360}{}{} } \end{tikzpicture} 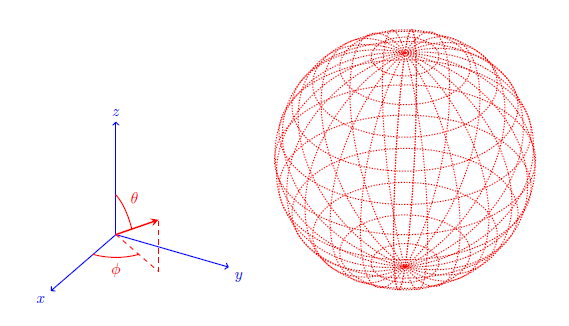
The left instance is an extension of the vector example shown earlier. An arc was added in the xy plane to illustrate the azimuthal angle, φ, and another arc was added to illustrate the polar angle, θ. In the correct example, a serial of circles are fatigued to correspond longitudinal and latitudinal lines on a sphere.
To make these examples, a few useful helper functions are used. Offset, the \tdplotsetthetaplanecoords{φ} function gives a convenient way of placing rotated coordinate frame such that the x'y' aeroplane is lined up to depict the polar angle, θ. Second, the \tdplotsinandcos{\sintheta}{\costheta}{θ} command takes the specified angle, θ (in degrees), and stores the sine and cosine value of that angle in the macros \sintheta and \costheta. Annotation that you can use whatever name in place of \sintheta and \costheta for your convenience.
Drawing Surfaces
Drawing lines and curves can be groovy fun, but what if you wanted to represent a solid object with opaque surfaces? With proper planning and conscientious consideration of which surfaces are fatigued starting time, you can render simple shapes.
\tdplotsetmaincoords{threescore}{125} \brainstorm{tikzpicture} [tdplot_main_coords, filigree/.style={very thin,grayness}, centrality/.fashion={->,blue,thick}, cube/.style={opacity=.5,very thick,make full=crimson}] %describe a grid in the x-y plane \foreach \x in {-0.5,0,...,2.v} \foreach \y in {-0.5,0,...,ii.5} { \draw[grid] (\10,-0.5) -- (\x,2.5); \draw[grid] (-0.5,\y) -- (2.5,\y); } %draw the axes \draw[axis] (0,0,0) -- (3,0,0) node[anchor=west]{$x$}; \draw[axis] (0,0,0) -- (0,3,0) node[anchor=west]{$y$}; \depict[axis] (0,0,0) -- (0,0,iii) node[ballast=west]{$z$}; %draw the bottom of the cube \draw[cube] (0,0,0) -- (0,ii,0) -- (2,2,0) -- (2,0,0) -- wheel; %depict the dorsum-right of the cube \draw[cube] (0,0,0) -- (0,2,0) -- (0,ii,ii) -- (0,0,two) -- cycle; %describe the back-left of the cube \draw[cube] (0,0,0) -- (2,0,0) -- (2,0,two) -- (0,0,2) -- cycle; %draw the front-right of the cube \draw[cube] (two,0,0) -- (2,2,0) -- (2,2,2) -- (2,0,two) -- wheel; %depict the front-left of the cube \draw[cube] (0,ii,0) -- (2,2,0) -- (two,2,2) -- (0,2,two) -- cycle; %draw the superlative of the cube \draw[cube] (0,0,2) -- (0,ii,2) -- (2,ii,2) -- (2,0,2) -- cycle; \end{tikzpicture} \tdplotsetmaincoords{60}{125} \brainstorm{tikzpicture}[ tdplot_main_coords, grid/.style={very thin,gray}, centrality/.style={->,blueish,thick}, cube/.style={very thick,fill=red}, cube hidden/.style={very thick,dashed}] %describe a grid in the 10-y plane \foreach \x in {-0.five,0,...,two.5} \foreach \y in {-0.5,0,...,2.v} { \draw[grid] (\10,-0.5) -- (\x,ii.5); \depict[grid] (-0.five,\y) -- (two.5,\y); } %draw the axes \draw[axis] (0,0,0) -- (three,0,0) node[ballast=w]{$x$}; \depict[axis] (0,0,0) -- (0,iii,0) node[anchor=west]{$y$}; \describe[axis] (0,0,0) -- (0,0,3) node[anchor=westward]{$z$}; %draw the front end-right of the cube \describe[cube] (two,0,0) -- (2,2,0) -- (2,2,2) -- (2,0,two) -- wheel; %depict the front-left of the cube \depict[cube] (0,2,0) -- (2,2,0) -- (ii,two,2) -- (0,2,2) -- bicycle; %draw the top of the cube \depict[cube] (0,0,2) -- (0,2,2) -- (2,2,2) -- (two,0,2) -- bicycle; %draw dashed lines to represent hidden edges \depict[cube hidden] (0,0,0) -- (2,0,0); \draw[cube hidden] (0,0,0) -- (0,two,0); \depict[cube hidden] (0,0,0) -- (0,0,ii); \cease{tikzpicture} 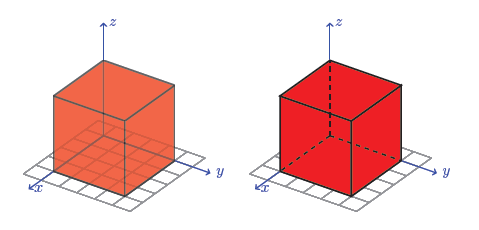
The left example uses fill color transparency to illustrate surfaces subconscious backside others. Here, the covered and back edges of the cube are distinguished by having the fill for the forepart surfaces drawn over pinnacle. The right instance has opaque front surfaces of the cube fatigued start, so the back edges are illustrated using dashed lines. In both situations, the order of cartoon depends on the perspective. If you change the orientation of the coordinate frame, you lot will demand to be careful well-nigh whether the drawing lodge needs to alter. In the case with dashed lines, y'all may even need to reassign roles to the components of the object.
Another example of surface plots is the \tdplotsphericalsurfaceplot command. This command was developed to allow me to plot complex spherical harmonics, where the radius and hue of the surface is plotted as a function of the polar and azimuthal angles.
\tdplotsetmaincoords{70}{135} \begin{tikzpicture}[scale=4,line bring together=bevel,tdplot_main_coords, fill opacity=.5] \pgfsetlinewidth{.2pt} \tdplotsphericalsurfaceplot[parametricfill]{72}{36}{sin(\tdplottheta)*cos(\tdplottheta)}{black}{\tdplotphi}% {\depict[color=blackness,thick,->] (0,0,0) -- (one,0,0) node[ballast=north due east]{$x$};}% {\draw[color=black,thick,->] (0,0,0) -- (0,1,0) node[anchor=northward west]{$y$};}% {\depict[color=black,thick,->] (0,0,0) -- (0,0,1) node[ballast=southward]{$z$};}% \finish{tikzpicture} 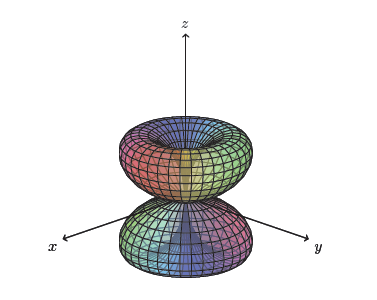
Here, I am plotting the function r = sin(θ)cos(θ), and using φ as the parameter to choose the surface fill up hue. The instructions for \tdplotsphericalsurfaceplot define the angular step sizes, the function to plot, the line style, the make full style, and instructions for drawing axes. Unlike the manual surface plot examples shown earlier, the \tdplotsphericalsurfaceplot command does the work of determining how to appropriately draw the surface so that surfaces and edges drawn on the back side are appropriately rendered below those on the forepart. The only downside with this is that it takes some time to return, then you may want to look into externalizing these figures.
Limitations
When drawing shapes in tikz-3dplot, but simple shapes like line segments and arcs behave properly, whereas more involved shapes similar rectangles and grids practice non adhere to the sense of rotated coordinate system. Let'south expect at the first example again, where we use the rectangle command to draw the acme and lesser of the cube, rather than a series of line segments.
\brainstorm{tikzpicture} %draw a grid in the 10-y plane \foreach \x in {-0.5,0,...,2.five} \foreach \y in {-0.5,0,...,two.5} { \draw[grey,very thin] (\10,-0.5) -- (\ten,2.five); \draw[grayness,very thin] (-0.5,\y) -- (2.v,\y); } %draw the axes \draw[->] (0,0,0) -- (3,0,0) node[ballast=w]{$ten$}; \draw[->] (0,0,0) -- (0,3,0) node[ballast=w]{$y$}; \describe[->] (0,0,0) -- (0,0,3) node[anchor=west]{$z$}; %draw the acme and bottom of the cube \draw[very thick] (0,0,0) rectangle (2,2,0); \describe[very thick] (0,0,two) rectangle (2,2,2); %draw the edges of the cube \draw[very thick] (0,0,0) -- (0,0,two); \draw[very thick] (0,ii,0) -- (0,2,2); \draw[very thick] (2,0,0) -- (two,0,ii); \describe[very thick] (2,two,0) -- (2,2,2); \cease{tikzpicture} \tdplotsetmaincoords{sixty}{125} \begin{tikzpicture}[tdplot_main_coords] %describe a grid in the x-y aeroplane \foreach \x in {-0.5,0,...,2.5} \foreach \y in {-0.5,0,...,two.v} { \draw[gray,very sparse] (\x,-0.5) -- (\x,2.5); \draw[grey,very thin] (-0.5,\y) -- (2.5,\y); } %draw the axes \describe[->] (0,0,0) -- (3,0,0) node[ballast=west]{$x$}; \draw[->] (0,0,0) -- (0,3,0) node[ballast=due west]{$y$}; \draw[->] (0,0,0) -- (0,0,3) node[ballast=due west]{$z$}; %draw the top and lesser of the cube \depict[very thick] (0,0,0) rectangle (ii,2,0); \depict[very thick] (0,0,ii) rectangle (ii,2,2); %depict the edges of the cube \draw[very thick] (0,0,0) -- (0,0,two); \depict[very thick] (0,2,0) -- (0,ii,2); \depict[very thick] (ii,0,0) -- (2,0,2); \draw[very thick] (2,2,0) -- (2,two,2); \end{tikzpicture} 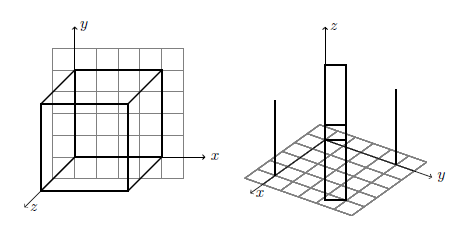
If you look advisedly at the rotated diagram, you'll discover that the rectangles are drawn with the correct beginning and end points, but the overall shape conforms to the original coordinate organization of the folio.
For More than Data
For more than information, I recommend you accept a look at the package, located at www.ctan.org/pkg/tikz-3dplot.
About the Author:Jeff Hein is the author of the tikz-3dplot packet. He maintains a blog for this package on tikz3dplot.wordpress.com.
Source: https://latex.net/tikz-3dplot/
Enviar um comentário for "How to Draw a Cartesian Plane in Latex"